Knowledge Representation in Bicategories of Relations

$\quad$ $\quad\implies\quad$

Evan Patterson
Stanford University, Statistics Department

AMS Fall Western Sectional Meeting
Special Session on Applied Category Theory
November 5, 2017

Knowledge representation (KR)

"An ontology is a specification of a conceptualization."
—Thomas Gruber, co-founder of Siri, Inc.

New applications motivating KR research:

• Semantic Web (RDF, OWL)
• Ontologies in biology and biomedicine (e.g. Gene Ontology)

Description logic (DL)

• Dominant formalism for KR today
• Basis for Web Ontology Language (OWL)
• Computationally tractable subset of first-order logic
• Basic entities:
  • concepts (classes)
  • roles (relations)
  • subsumptions (containments) of concepts/roles

DL examples

Syntax and semantics of a few concept constructors:

$$ \begin{align} C \sqcap D \qquad&\stackrel{\mathrm{FOL}}{\leadsto}\qquad (C \sqcap D)(x) \ \leftrightarrow\ C(x) \wedge D(x) \\ \forall R.C \qquad&\stackrel{\mathrm{FOL}}{\leadsto}\qquad (\forall R.C)(x) \ \leftrightarrow\ \forall y. R(x,y) \wedge C(y) \\ \exists R.\top \qquad&\stackrel{\mathrm{FOL}}{\leadsto}\qquad (\exists R.\top)(x) \ \leftrightarrow\ \exists y. R(x,y) % \exists R.C % \qquad&\stackrel{\mathrm{FOL}}{\leadsto}\qquad % (\exists R.C)(x) \ \leftrightarrow\ \exists y. R(x,y) \wedge C(y) \end{align} $$

Syntax and semantics of concept subsumption:

$$ C \sqsubseteq D \qquad\stackrel{\mathrm{FOL}}{\leadsto}\qquad \forall x. C(x) \rightarrow D(x) $$

Ontology logs (ologs)

• Spivak and Kent (2012) introduce ontology logs
• Ologs are a categorical framework for KR
• A (functional) olog $\mathcal{C}$ is just a finitely presented category:
  • Objects are types in the subject-matter domain
  • Morphisms are aspects or properties
  • Commutative diagrams encode facts about the domain
• Instance data for an olog is a functor $\mathcal{C} \to \mathbf{Set}$
• Further expressivity is achieved via
  • Limits aka layouts
  • Colimits aka grouping

Example olog

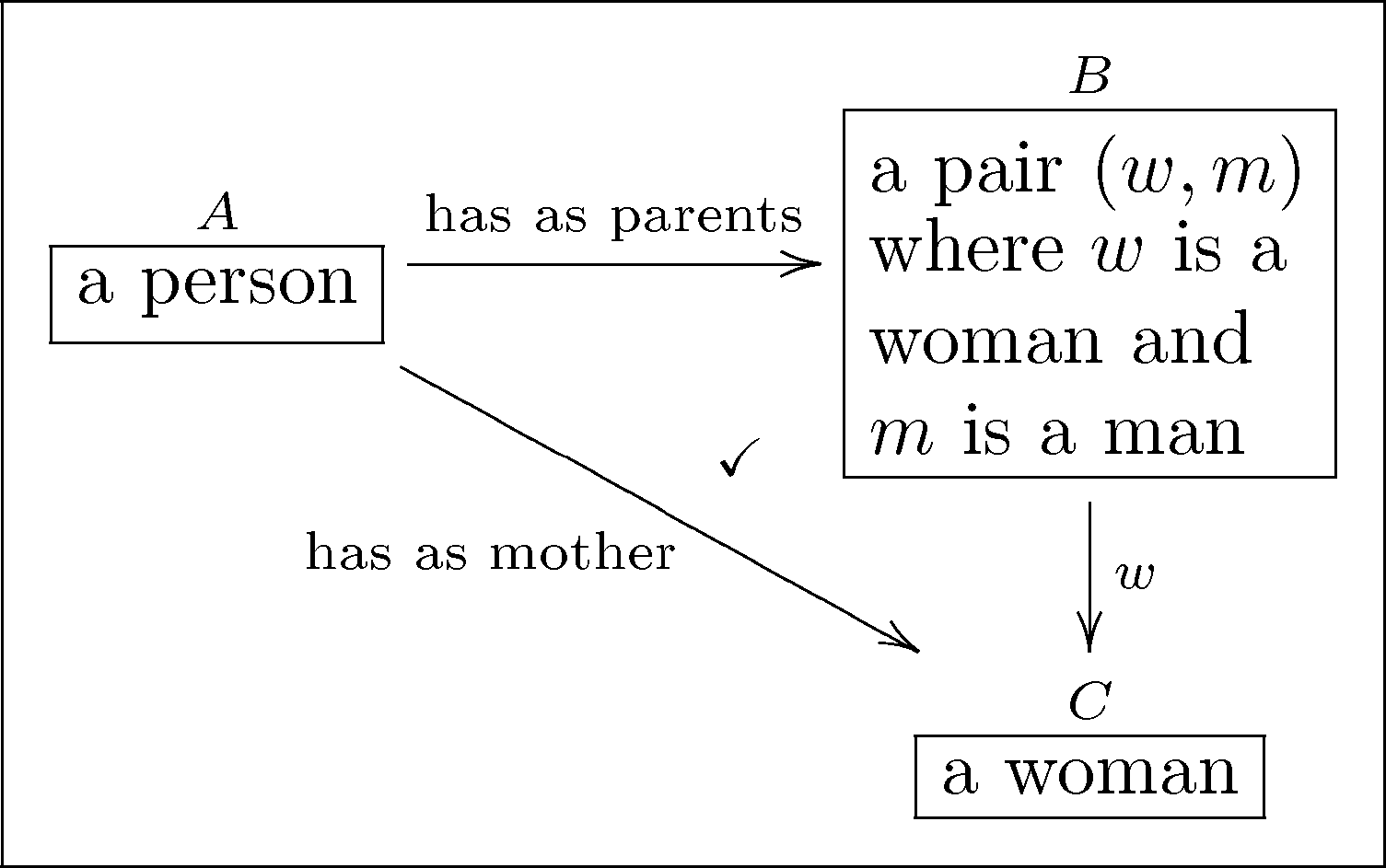
Relational ologs

• Ologs are based on Set, the category of sets and functions
• But description logic is based on relations, not functions
• So what about Rel, the category of sets and relations?

This project is about relational ologs, a categorical-relational framework for knowledge representation.

Goals:

1. Explore relationship between logical and algebraic KR
2. Develop distinctive advantages of categorical KR

Advantages of relational ologs

In contrast to DL, relational ologs provide

1. An explicit type system, via objects
2. A flexible notion of instance data that cleanly separates universal and particular knowledge, via functors
3. An intuitive graphical syntax, via string diagrams

All these features emerge automatically from the categorical framework.

The category of relations

Rel, the category of sets and relations, is a monoidal category.

Composition: Given relations $R: X \to Y$ and $S: Y \to Z$,

$\quad$ $\quad:=\quad \{(x,z): \exists y \in Y. xRy \wedge ySz\}$

Cartesian product: Given relations $R: X \to Y$ and $S: Z \to W$,

$\quad$ $\quad:=\quad \{((x,z),(y,w)): xRy \wedge zSw\}$

Rel as a monoidal category

Dagger: Given a relation $R: X \to Y$,

$\quad$ $\quad:=\quad \{(y,x): yRx\}$

Diagonals: For every set $X$,

$\quad$ $\quad:=\quad \{(x,(x',x'')): x=x' \wedge x=x''\}$
$\quad$ $\quad:=\quad \{(x,*): x \in X\}$

Together they define a family of commutative special $\dagger$-Frobenius monoids.

Rel as a monoidal category

Rel is also a dagger compact category with units and counits defined by

$\quad$ $\quad:=\quad$ $\quad=\quad \{(*,(x,x')): x = x'\}$
$\quad$ $\quad:=\quad$ $\quad=\quad \{((x,x'),*): x = x'\}$

Rel as a 2-category

Rel is a locally posetal 2-category: given relations $R,S: X \to Y$,

$$ R \implies S \qquad\text{iff}\qquad R \subseteq S. $$

2-morphisms correspond to subsumptions in DL.

Examples from description logic

Intersection of $R,S: X \to Y$:

$\quad R \sqcap S \quad=\quad$

Limited existential quantification of $R:X \to Y$:

$\quad \exists R.\top \quad=\quad$

Abstract categories of relations

• How to make a categorical-relational KR system?
• Rel is not sufficient
• Need a finitary specification language
• Two categorical abstractions of relational algebra in literature
  1. Allegories (Freyd & Scedrov)
  2. Bicategories of relations (Carboni & Walters)

Bicategories of relations

A bicategory of relations is a locally posetal 2-category $\mathcal{B}$ that is also a symmetric monoidal category $(\mathcal{B},\otimes,I)$ with diagonals $(X,\Delta_X,\lozenge_X)_{X \in \mathcal{B}}$, such that

• every morphism $R: X \to Y$ is a lax comonoid homomorphism:

$\qquad$ $\quad\implies\quad$

$\qquad$ $\quad\implies\quad$

• $\Delta_X$ and $\lozenge_X$ have right adjoints, $\nabla_X := \Delta_X^*$ and $\square_X := \lozenge_X^*$
• the Frobenius equation holds, making $(X,\Delta_X,\lozenge_X,\nabla_X,\square_X)$ into a Frobenius monoid

Relational ologs

A relational olog is a finitely presented bicategory of relations.

"Finitely presented" means generated by

• a finite set of basic types or object generators
• a finite set of basic relations or morphism generators
• a finite set of subsumbtion axioms or 2-morphisms generators

Instance data

Instance data for a relational olog $\mathcal{B}$ is a functor $\mathcal{B} \to \mathcal{D}$ in $\mathbf{BiRel}$, where the data category $\mathcal{D}$ is, e.g.,

• $\mathbf{Rel}$ or $\mathbf{FinRel}$ (the "default")

$$ R = \begin{array}{|c|c|} \hline X & Y \\\hline 1 & 2 \\ 2 & 1 \\ 3 & 3 \\\hline \end{array} $$

• $\mathbf{Mat}(\mathbb{B})$, the category of boolean matrices

$$ R = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} $$

• $\mathbf{VectRel}_k$, the category of linear relations

Algebra and logic

• Bicategories of relations are
  • informally related to description logic
  • formally connected to regular logic
• Regular logic: fragment of first-order logic with connectives $$\exists, \wedge, \top, =$$
• Correspondence: bicategory of relations $\leftrightarrow$ regular theories
• Result belongs to categorical logic
  • In style of: CCCs $\leftrightarrow$ lambda calculus theories
  • No subobjects!

Classifying category

Every regular theory $\mathbb{T}$ has a classifying category $\mathrm{Cl}(\mathbb{T})$, a bicategory of relations with

• objects = (equivalence classes of) contexts $$[x: A] = [x_1: A_1,\dots, x_n: A_n]$$
• morphisms = (equivalence classes of) formulas in context $$[x: A; y: B\ |\ \varphi]$$

Internal language

Every (small) bicategory of relations $\mathcal{B}$ has an internal language $\mathrm{Lang}(\mathcal{B})$, a regular theory with

• types = objects of $\mathcal{B}$
• relation symbols = morphisms of $\mathcal{B}$
• theorems = 2-morphisms (subsumptions) of $\mathcal{B}$

Theorem

For every (small) bicategory of relations $\mathcal{B}$, there is an equivalence of categories $$ \mathrm{Cl}(\mathrm{Lang}(\mathcal{B})) \simeq \mathcal{B} \qquad\text{in}\qquad \mathbf{BiRel}. $$

Conclusion

Extensions: We have products but what about sums?

• Classical disjunction: distributive bicategories of relations
• Linear sum: abelian bicategories of relations

Future work

• Automated inference
  • exact
  • approximate
• Computer implementation (see Catlab)

Thanks!

Paper: E. Patterson, "Knowledge Representation in Bicategories of Relations", 2017 [arXiv]

Background reading:

• Ologs: D.I. Spivak & R.E. Kent, "Ologs: A Categorical Framework for Knowledge Representation", 2011 [arXiv, DOI]
• Description logic: M. Krötzsch, F. Simancik, I. Horrocks, "A Description Logic Primer", 2012 [arXiv]
• Rel: B. Coecke & E.O. Paquette, "Categories for the Practicising Physicist", 2010 [arXiv]
• Bicategories of relations: A. Carboni & R.F.C. Walters, "Cartesian Bicategories I", 1987