Knowledge Representation in Bicategories of Relations¶
$\quad$
$\quad\implies\quad$
Evan Patterson
Stanford University, Statistics Department
AMS Fall Western Sectional Meeting
Special Session on Applied Category Theory
November 5, 2017
Knowledge representation (KR)¶
"An ontology is a specification of a conceptualization."
—Thomas Gruber, co-founder of Siri, Inc.
New applications motivating KR research:
- Semantic Web (RDF, OWL)
- Ontologies in biology and biomedicine (e.g. Gene Ontology)
Description logic (DL)¶
- Dominant formalism for KR today
- Basis for Web Ontology Language (OWL)
- Computationally tractable subset of first-order logic
- Basic entities:
- concepts (classes)
- roles (relations)
- subsumptions (containments) of concepts/roles
DL examples¶
Syntax and semantics of a few concept constructors:
$$
\begin{align}
C \sqcap D
\qquad&\stackrel{\mathrm{FOL}}{\leadsto}\qquad
(C \sqcap D)(x) \ \leftrightarrow\ C(x) \wedge D(x) \\
\forall R.C
\qquad&\stackrel{\mathrm{FOL}}{\leadsto}\qquad
(\forall R.C)(x) \ \leftrightarrow\ \forall y. R(x,y) \wedge C(y) \\
\exists R.\top
\qquad&\stackrel{\mathrm{FOL}}{\leadsto}\qquad
(\exists R.\top)(x) \ \leftrightarrow\ \exists y. R(x,y)
% \exists R.C
% \qquad&\stackrel{\mathrm{FOL}}{\leadsto}\qquad
% (\exists R.C)(x) \ \leftrightarrow\ \exists y. R(x,y) \wedge C(y)
\end{align}
$$
Syntax and semantics of concept subsumption:
$$
C \sqsubseteq D
\qquad\stackrel{\mathrm{FOL}}{\leadsto}\qquad
\forall x. C(x) \rightarrow D(x)
$$
Ontology logs (ologs)¶
- Spivak and Kent (2012) introduce ontology logs
- Ologs are a categorical framework for KR
- A (functional) olog $\mathcal{C}$ is just a finitely presented category:
- Objects are types in the subject-matter domain
- Morphisms are aspects or properties
- Commutative diagrams encode facts about the domain
- Instance data for an olog is a functor $\mathcal{C} \to \mathbf{Set}$
- Further expressivity is achieved via
- Limits aka layouts
- Colimits aka grouping
Example olog¶
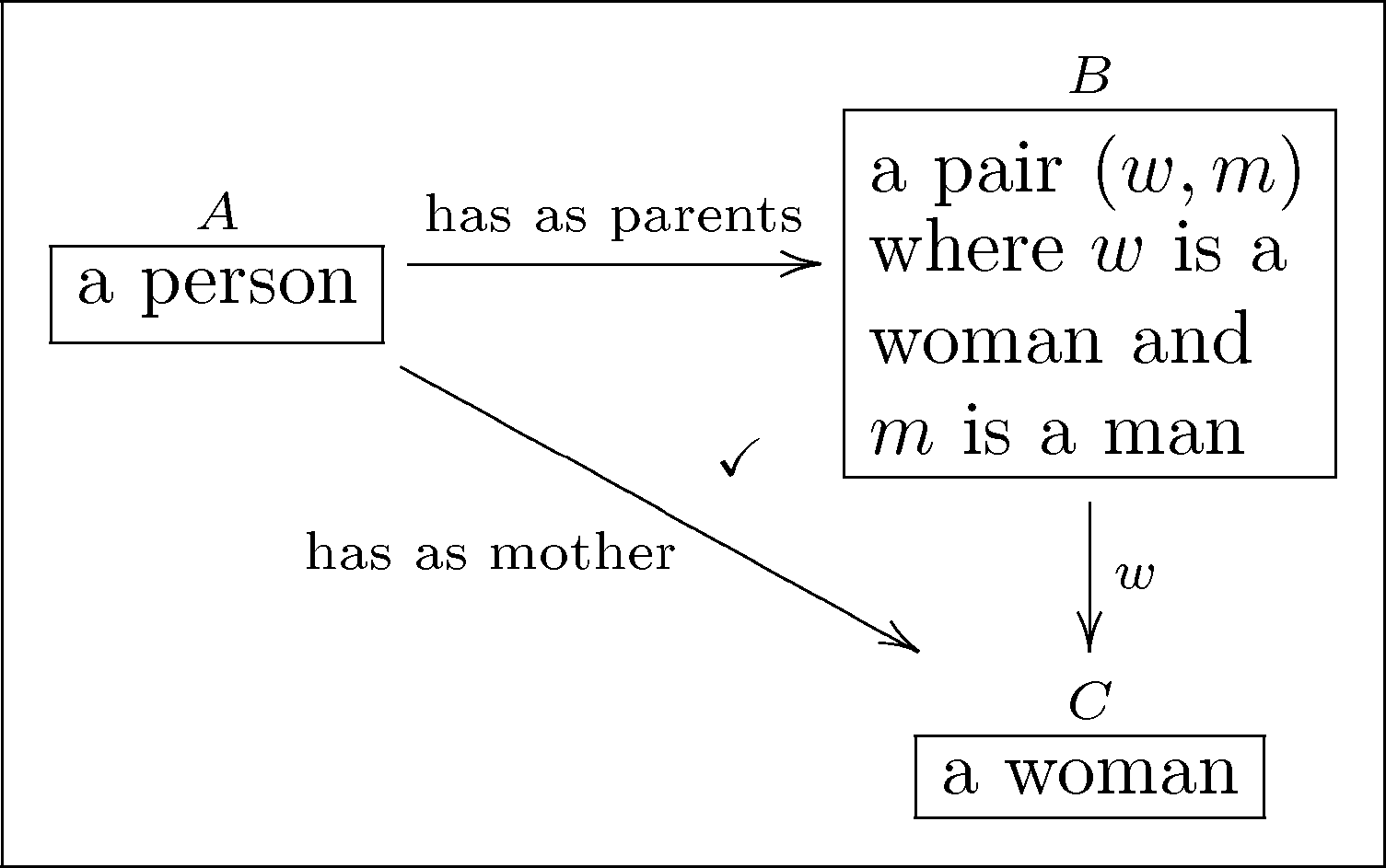
Relational ologs¶
- Ologs are based on Set, the category of sets and functions
- But description logic is based on relations, not functions
- So what about Rel, the category of sets and relations?
This project is about relational ologs, a categorical-relational framework for knowledge representation.
Goals:
- Explore relationship between logical and algebraic KR
- Develop distinctive advantages of categorical KR
Advantages of relational ologs¶
In contrast to DL, relational ologs provide
- An explicit type system, via objects
- A flexible notion of instance data that cleanly separates universal and particular knowledge, via functors
- An intuitive graphical syntax, via string diagrams
All these features emerge automatically from the categorical framework.
The category of relations¶
Rel, the category of sets and relations, is a monoidal category.
Composition: Given relations $R: X \to Y$ and $S: Y \to Z$,
$\quad$
$\quad:=\quad \{(x,z): \exists y \in Y. xRy \wedge ySz\}$
Cartesian product: Given relations $R: X \to Y$ and $S: Z \to W$,
$\quad$
$\quad:=\quad \{((x,z),(y,w)): xRy \wedge zSw\}$
Rel as a monoidal category¶
Dagger: Given a relation $R: X \to Y$,
$\quad$
$\quad:=\quad \{(y,x): yRx\}$
Diagonals: For every set $X$,
$\quad$
$\quad:=\quad \{(x,(x',x'')): x=x' \wedge x=x''\}$
$\quad$
$\quad:=\quad \{(x,*): x \in X\}$
Together they define a family of commutative special $\dagger$-Frobenius monoids.
Rel as a monoidal category¶
Rel is also a dagger compact category with units and counits defined by
$\quad$
$\quad:=\quad$
$\quad=\quad \{(*,(x,x')): x = x'\}$
$\quad$
$\quad:=\quad$
$\quad=\quad \{((x,x'),*): x = x'\}$
Rel as a 2-category¶
Rel is a locally posetal 2-category: given relations $R,S: X \to Y$,
$$
R \implies S \qquad\text{iff}\qquad R \subseteq S.
$$
2-morphisms correspond to subsumptions in DL.
Examples from description logic¶
Intersection of $R,S: X \to Y$:
$\quad R \sqcap S \quad=\quad$
Limited existential quantification of $R:X \to Y$:
$\quad \exists R.\top \quad=\quad$
Abstract categories of relations¶
- How to make a categorical-relational KR system?
- Rel is not sufficient
- Need a finitary specification language
- Two categorical abstractions of relational algebra in literature
- Allegories (Freyd & Scedrov)
- Bicategories of relations (Carboni & Walters)
Bicategories of relations¶
A bicategory of relations is a locally posetal 2-category $\mathcal{B}$ that is also a symmetric monoidal category $(\mathcal{B},\otimes,I)$ with diagonals $(X,\Delta_X,\lozenge_X)_{X \in \mathcal{B}}$, such that
- every morphism $R: X \to Y$ is a lax comonoid homomorphism:
$\qquad$
$\quad\implies\quad$
$\qquad$
$\quad\implies\quad$
- $\Delta_X$ and $\lozenge_X$ have right adjoints, $\nabla_X := \Delta_X^*$ and $\square_X := \lozenge_X^*$
- the Frobenius equation holds, making $(X,\Delta_X,\lozenge_X,\nabla_X,\square_X)$ into a Frobenius monoid
Relational ologs¶
A relational olog is a finitely presented bicategory of relations.
"Finitely presented" means generated by
- a finite set of basic types or object generators
- a finite set of basic relations or morphism generators
- a finite set of subsumbtion axioms or 2-morphisms generators
Instance data¶
Instance data for a relational olog $\mathcal{B}$ is a functor $\mathcal{B} \to \mathcal{D}$ in $\mathbf{BiRel}$, where the data category $\mathcal{D}$ is, e.g.,
- $\mathbf{Rel}$ or $\mathbf{FinRel}$ (the "default")
$$ R = \begin{array}{|c|c|} \hline X & Y \\\hline 1 & 2 \\ 2 & 1 \\ 3 & 3 \\\hline \end{array} $$
- $\mathbf{Mat}(\mathbb{B})$, the category of boolean matrices
$$ R = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} $$
- $\mathbf{VectRel}_k$, the category of linear relations
Algebra and logic¶
- Bicategories of relations are
- informally related to description logic
- formally connected to regular logic
- Regular logic: fragment of first-order logic with connectives $$\exists, \wedge, \top, =$$
- Correspondence: bicategory of relations $\leftrightarrow$ regular theories
- Result belongs to categorical logic
- In style of: CCCs $\leftrightarrow$ lambda calculus theories
- No subobjects!
Classifying category¶
Every regular theory $\mathbb{T}$ has a classifying category $\mathrm{Cl}(\mathbb{T})$, a bicategory of relations with
- objects = (equivalence classes of) contexts $$[x: A] = [x_1: A_1,\dots, x_n: A_n]$$
- morphisms = (equivalence classes of) formulas in context $$[x: A; y: B\ |\ \varphi]$$
Internal language¶
Every (small) bicategory of relations $\mathcal{B}$ has an internal language $\mathrm{Lang}(\mathcal{B})$, a regular theory with
- types = objects of $\mathcal{B}$
- relation symbols = morphisms of $\mathcal{B}$
- theorems = 2-morphisms (subsumptions) of $\mathcal{B}$
Theorem¶
For every (small) bicategory of relations $\mathcal{B}$, there is an equivalence of categories $$ \mathrm{Cl}(\mathrm{Lang}(\mathcal{B})) \simeq \mathcal{B} \qquad\text{in}\qquad \mathbf{BiRel}. $$
Thanks!¶
Paper: E. Patterson, "Knowledge Representation in Bicategories of Relations", 2017 [arXiv]
Background reading:
- Ologs: D.I. Spivak & R.E. Kent, "Ologs: A Categorical Framework for Knowledge Representation", 2011 [arXiv, DOI]
- Description logic: M. Krötzsch, F. Simancik, I. Horrocks, "A Description Logic Primer", 2012 [arXiv]
- Rel: B. Coecke & E.O. Paquette, "Categories for the Practicising Physicist", 2010 [arXiv]
- Bicategories of relations: A. Carboni & R.F.C. Walters, "Cartesian Bicategories I", 1987