Description logic (DL)¶

• Dominant formalism for KR today
• Basis for Web Ontology Language (OWL)
• Computationally tractable subset of first-order logic

Example concept constructors: C⊓DFOL⇝(C⊓D)(x)↔(C(x)∧D(x))∀R.CFOL⇝(∀R.C)(x)↔(∀y.R(x,y)∧C(y))∃R.⊤FOL⇝(∃R.⊤)(x)↔(∃y.R(x,y))

Ontology logs (ologs)¶

• Spivak and Kent (2012) introduce ontology logs
• Categorical framework for KR

Relational ologs¶

• Ologs are based on Set, the category of sets and functions
• What about Rel, the category of sets and relations?
• This project: relational ologs, a categorical-relational framework for KR
• Objectives:
  1. Understand relationship between logical and algebraic approaches to KR
  2. Develop distinctive advantages of categorical KR

Two basic operations in Rel¶

Composition: Given R:X→Y and S:Y→Z,

:={(x,z):∃y∈Y.xRy∧ySz}

Cartesian product: Given R:X→Y and S:Z→W,

:={((x,z),(y,w)):xRy∧zSw}

Dagger and diagonals in Rel¶

Dagger: Given R:X→Y,

:={(y,x):yRx}

Diagonals: For every set X,

:={(x,(x′,x″)):x=x′∧x=x″}

:={(x,∗):x∈X}

Examples from description logic¶

Intersection of R,S:X→Y:

R⊓S=

Limited existential quantification of R:X→Y:

∃R.⊤=

Rel as a 2-category¶

Rel is a locally posetal 2-category: given relations R,S:X→Y,

R⟹SiffR⊆S.

2-morphisms correspond to subsumption in description logic.

Bicategories of relations¶

A bicategory of relations is a locally posetal 2-category B that is also a symmetric monoidal category (B,⊗,I) with diagonals (X,ΔX,◊X)X∈B subject to several axioms.

Axioms ensure that

• monoidal product and diagonals behave like the Cartesian product
• 2-morphisms interact properly with other structures

Relational olog¶

A relational olog is a finitely presented bicategory of relations.

"Finitely presented" means generated by

• a finite set of basic types or object generators
• a finite set of basic relations or morphism generators
• a finite set of subsumbtion axioms or 2-morphisms generators

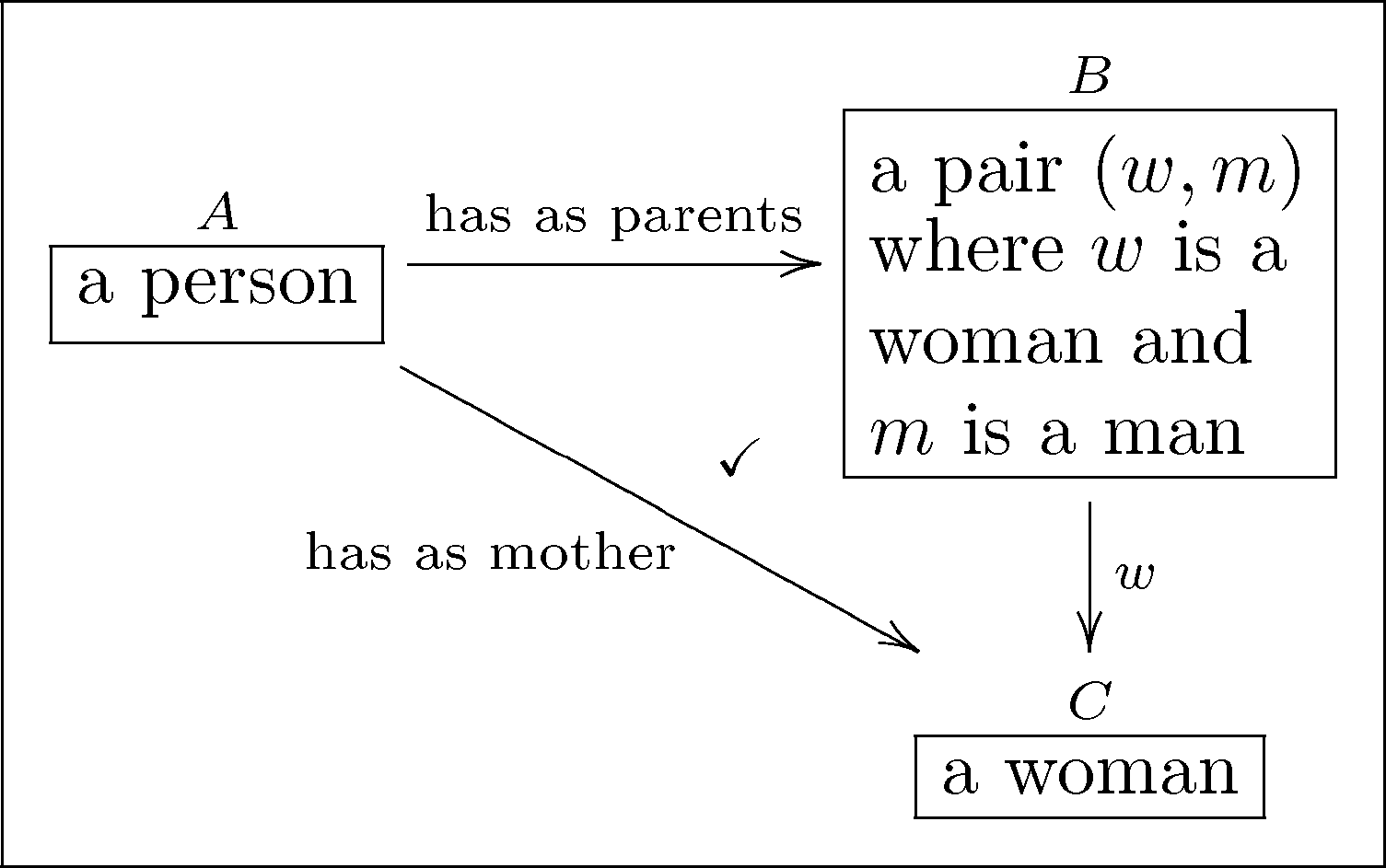
Example: Friend of a friend¶

• Basic types: "Person", "Organization"
• Basic relations: "knows", "friend of", "works at", etc.
• Example subsumption axiom

⟹