Realizing applied category theory in Julia¶
An introduction to Catlab.jl, an experimental framework for ACT¶
Evan Patterson
Stanford University, Statistics Department
MIT (Applied) Categories Seminar
January 16, 2020
Applied category theory in 2020¶
Applications of category theory began in logic/type theory but have now spread to
- Quantum mechanics
- Chemistry (reaction networks, Petri nets)
- Databases and knowledge representation
- Control theory and robotics
- Probability and statistics
- ...
Why? CT offers a unifying and widely applicable toolbox for building mathematical models of compositional phenomena.
But where are the tools?¶
In applied math, the math is only half the story.
Applied mathematics must ultimately feed back into better scientific and computational methods.
Software is a big part of this, but software tools for ACT are early and fragmented.
Question: How do we usefully realize the mathematical models of ACT on a computer?
Two views on categories and software¶
Designing with categories: CT informing the design, architecture, and implementation of computer programs, in any domain
Slogan: "Design patterns, but better"
Computing on categories: data structures and algorithms for computing with objects and morphisms in categories
Slogan: "Computer algebra of categories" or "computational category theory"
Both are valuable, but they are not the same. In principle, they are orthogonal.
This talk is about computational category theory (mostly).
Some specific features:
- Work with symbolic expressions for objects and morphisms
- Create, manipulate, and visualize wiring diagrams for morphisms
- Generate efficient Julia programs for algorithms expressed categorically
Overview: representing morphisms in monoidal categories¶
As of today, one of Catlab's most powerful capabilities is transforming between different computational representations of morphisms in symmetric monoidal categories.
Yet Julia is also practical:
- Designed to be fast, thanks to JIT (just-in-time) compiler
- Growing force in conventional applied math community:
- Numerical linear algebra
- Differential equations
- Optimization
- Statistics and machine learning
Some other projects in computational category theory¶
- Cateno by Jason Morton, in Julia
- Prototype, unmaintained since 2015
- Early inspiration for Catlab
- In turn, draws inspiration from Haskell type classes
- Categorical Query Language by Conexus AI (AGPL/proprietary)
- Solves word problems in finitely presented categories
- Statebox (AGPL/proprietary)
- Compositional programming with formal verification
- Rewriting and proof assistants for monoidal/higher categories:
- Quantomatic by Aleks Kissinger et al
- Globular by Jamie Vicary et al
- Cartographer by Pawel Sobocinski et al
Talk outline¶
- Major features
- Signatures, instances, and symbolic expressions
- Wiring diagrams
- Generating and parsing Julia programs
- Applications
- Future directions
Signatures, instances, and symbolic expressions¶
In Catlab, you can define signatures of algebraic structures (@signature macro).
module Sandbox # Encapsulate in module to avoid name conflicts later
export dom, codom, id, compose
using Catlab
@signature Category(Ob,Hom) begin
Ob::TYPE
Hom(dom::Ob,codom::Ob)::TYPE
id(A::Ob)::Hom(A,A)
compose(f::Hom(A,B), g::Hom(B,C))::Hom(A,C) <= (A::Ob, B::Ob, C::Ob)
end
end
Main.Sandbox
Note: Usually use Category from "standard library" (Catlab.Doctrines)
Signature interface¶
Signatures define generic functions in Julia.
methodswith(Sandbox.Category.Ob, Sandbox)
- id(A::Main.Sandbox.Category.Ob) in Main.Sandbox
methodswith(Sandbox.Category.Hom, Sandbox)
- codom(::Main.Sandbox.Category.Hom) in Main.Sandbox
- compose(f::Main.Sandbox.Category.Hom, g::Main.Sandbox.Category.Hom) in Main.Sandbox
- dom(::Main.Sandbox.Category.Hom) in Main.Sandbox
Instances¶
Two ways to instantiate a signature:
- As Julia functions on concrete data types (
@instancemacro or standard Julia) - As typed systems of symbolic expressions (
@syntaxmacro)
Instance: category of matrices¶
Instance of Category with (element type, dimension) pairs as objects and matrices as morphisms.
using Catlab, Catlab.Doctrines
import Catlab.Doctrines: Ob, Hom, dom, codom, id, compose, ⋅, ∘
using LinearAlgebra: I
struct MatrixDomain
eltype::Type
dim::Int
end
@instance Category(MatrixDomain, Matrix) begin
dom(M::Matrix) = MatrixDomain(eltype(M), size(M,1))
codom(M::Matrix) = MatrixDomain(eltype(M), size(M,2))
id(m::MatrixDomain) = Matrix{m.eltype}(I, m.dim, m.dim)
compose(M::Matrix, N::Matrix) = M*N
end
Instance: Category of matrices¶
M = [0 1; -1 0]
2×2 Array{Int64,2}:
0 1
-1 0
compose(M,M)
2×2 Array{Int64,2}:
-1 0
0 -1
id(dom(M))
2×2 Array{Int64,2}:
1 0
0 1
Symbolic expressions¶
Automatically generate system of symbolic expressions for Category.
@syntax CategoryExprs(ObExpr, HomExpr) Category begin
# Empty, so no simplification logic!
end
A, B, C, D = Ob(CategoryExprs, :A, :B, :C, :D)
f, g, h = Hom(:f, A, B), Hom(:g, B, C), Hom(:h, C, D)
f
compose(f,g)
compose(compose(f,g),h)
Symbolic expressions¶
Expression types¶
[ expr => typeof(expr) for expr in [A, f, id(A), compose(f,g) ] ]
4-element Array{Pair{A,DataType} where A,1}:
A => Main.CategoryExprs.Ob{:generator}
f => Main.CategoryExprs.Hom{:generator}
id(A) => Main.CategoryExprs.Hom{:id}
compose(f,g) => Main.CategoryExprs.Hom{:compose}
Unicode operators¶
f⋅g == compose(f,g)
true
g∘f == compose(f,g)
true
Simplification of symbolic expressions¶
By default, no simplification or normalization is performed.
(f⋅g)⋅h == f⋅(g⋅h)
false
But we can define symbolic expressions that normalize at construction.
@syntax NormalizingCategoryExprs(ObExpr, HomExpr) Category begin
compose(f::Hom, g::Hom) = associate_unit(new(f,g), id)
end
A, B, C, D = Ob(NormalizingCategoryExprs, :A, :B, :C, :D)
f, g, h = Hom(:f, A, B), Hom(:g, B, C), Hom(:h, C, D);
Note: Rewriting function associate_unit is built-in. You can also define your own.
(f⋅g)⋅h == f⋅(g⋅h)
true
id(A)⋅f == f && f⋅id(B) == f
true
Unbiased representation¶
args(f⋅g⋅h)
3-element Array{Main.NormalizingCategoryExprs.Hom{:generator},1}:
f
g
h
Math interlude: generalized algebraic theories (GATs)¶
Signatures are based on GATs (Cartmell 1978; Cartmell 1986)
- GATs = algebraic theories + simple dependent types
- Same expressivity as esentially algebraic theories (Freyd 1972)
- Minimal logical system for axiomatizing categorical doctrines
Caveat: Catlab only supports signature of theory; axioms for the future.
Wanted: Math and data structures for treating GATs, or doctrines, as data.
Wiring diagrams¶
Wiring diagrams, also known as
- string diagrams in physics and CT
- port graphs in computer science,
are a graphical syntax for morphisms in symmetric monoidal categories
(Spivak 2013; Rupel, Spivak 2013; Yau 2018).
Two kinds of wiring diagrams¶
- Combinatorial: Wiring diagrams as data structure, no geometry (
Catlab.WiringDiagrams) - Topological: Wiring diagrams as visualization, embedded in the plane (
Catlab.Graphics)
By default, "wiring diagram" has the first meaning.
Another distinction: Catlab has extensive support for directed wiring diagrams.
Undirected wiring diagrams are planned for the future.
Wiring diagrams as a data structure¶
Wiring diagrams are built on top of digraphs from LightGraphs.jl:
- Each box corresponds to a vertex
- Two special vertices for inputs/outputs of outer box
- Arbitrary metadata on boxes, ports, and wires
Two interfaces for wiring diagrams:
- Imperative: Mutate wiring diagram by adding/removing boxes and wires
- Categorical: Construct new diagrams from old by composing, tensoring, etc
Imperative interface for wiring diagrams¶
Manually constructing the wiring diagram visualized above:
using Catlab.WiringDiagrams
d = WiringDiagram([:A,:A], [:C,:C])
fv = add_box!(d, Box(:f, [:A], [:B]))
gv = add_box!(d, Box(:g, [:A], [:B]))
hv = add_box!(d, Box(:h, [:B,:B], [:C,:C]))
add_wires!(d, [ (input_id(d),1) => (fv,1), (input_id(d),2) => (gv,1),
(fv,1) => (hv,2), (gv,1) => (hv,1),
(hv,1) => (output_id(d),2), (hv,2) => (output_id(d),1) ])
d
WiringDiagram([:A,:A], [:C,:C],
[ 1 => {inputs},
2 => {outputs},
3 => Box(:f, [:A], [:B]),
4 => Box(:g, [:A], [:B]),
5 => Box(:h, [:B,:B], [:C,:C]) ],
[ Wire((1,1) => (3,1)),
Wire((1,2) => (4,1)),
Wire((3,1) => (5,2)),
Wire((4,1) => (5,1)),
Wire((5,1) => (2,2)),
Wire((5,2) => (2,1)) ])
Wiring diagrams as a monoidal category¶
Making the same diagram, compositionally:
A, B, C = Ports([:A]), Ports([:B]), Ports([:C])
f = singleton_diagram(Box(:f, A, B))
g = singleton_diagram(Box(:g, A, B))
h = singleton_diagram(Box(:h, B⊗B, C⊗C))
(f⊗g)⋅braid(B,B)⋅h⋅braid(C,C) == d
true
- All wiring diagrams are an instance of
SymmetricMonoidalCategory - Extra structure by parametrizing the base type, e.g.,
WiringDiagram{CartesianCategory.Hom}
Wiring diagrams as an operad¶
The fundamental operation is substitution of diagrams for boxes (substitute), aka operadic composition (ocompose).
Example: Implementing compose for wiring diagrams
function compose(f::WiringDiagram, g::WiringDiagram)
d = WiringDiagram(dom(f), codom(g))
fv, gv = add_box!(d, f), add_box!(d, g)
add_wires!(d, ((input_id(d),i) => (fv,i) for i in eachindex(dom(f))))
add_wires!(d, ((fv,i) => (gv,i) for i in eachindex(codom(f))))
add_wires!(d, ((gv,i) => (output_id(d),i) for i in eachindex(codom(g))))
substitute(d, [fv, gv])
end
Inverse of substitution is encapsulation of subdiagrams (encapsulate).
Wiring diagrams and morphism expressions¶
Morphism expressions → wiring diagrams:
- Easy
- Uniquely defined
- One-liner using generic
functorfrom expressions to another instance
Wiring diagrams → morphism expressions:
- Not easy
- Not uniquely defined (interchange law!)
- Algorithm inspired by series-parallel digraphs (Valdes et al 1982; Mitchell 2004)
Caveat: Need to make math out of this algorithm!
Normalization by round-tripping?¶
Decomposition algorithm maximizes parallelism (prefers ∘ over ⊗).
roundtrip(expr) = to_hom_expr(FreeCartesianCategory, to_wiring_diagram(expr))
A, B, C = Ob(FreeCartesianCategory, :A, :B, :C)
f, g, h, k = Hom(:f, A, B), Hom(:g, B, C), Hom(:h, A, B), Hom(:k, B, C)
expr = compose(otimes(f,h), otimes(g,k))
expr2 = roundtrip(expr)
roundtrip(expr2) == expr2
true
Normalization by round-tripping?¶
Implicitly uses coherence axioms for copying, deleting, etc.
mcopy(otimes(A,B))
roundtrip(mcopy(otimes(A,B)))
delete(otimes(A,B))
roundtrip(delete(otimes(A,B)))
Visualizing wiring diagrams¶
Wiring diagrams in Graphviz¶
using Catlab.Graphics
to_graphviz(d, orientation=LeftToRight)
to_graphviz(d, orientation=TopToBottom, labels=true, label_attr=:taillabel)
Wiring diagrams in Compose.jl/TikZ¶
using Compose: fill, stroke
to_composejl(FreeSymmetricMonoidalCategory, d,
box_props=[fill("lavender"),stroke("black")])
to_tikz(FreeSymmetricMonoidalCategory, d,
labels=true, labels_pos=0.25, arrowtip="Latex", arrowtip_pos=1.0)
Serializing wiring diagrams¶
Read and write wiring diagrams as:
- XML
- Conforms to GraphML standard
- JSON
Warning: No standards in this area, so interoperability is limited.
Generating and parsing Julia code¶
Catlab can transform Julia programs to/from other representations of morphisms.
Convenient to specify available functions by presenting a cartesian monoidal category.
@present TrigFunctions(FreeCartesianCategory) begin
R::Ob # Real numbers
sin::Hom(R,R)
cos::Hom(R,R)
(+)::Hom(otimes(R,R),R)
(*)::Hom(otimes(R,R),R)
end
generator(TrigFunctions, :+)
Generating Julia programs from morphism expressions¶
Functorial compilation of morphism expression into Julia function:
gen(name::Symbol) = generator(TrigFunctions, name)
expr = compose(mcopy(gen(:R)), otimes(gen(:sin),gen(:cos)), gen(:*))
using Catlab.Programs
compile_expr(expr, name=:my_trig_polynomial, args=[:x])
:(function my_trig_polynomial(x)
v1 = sin(x)
v2 = cos(x)
v3 = v1 * v2
return v3
end)
Parsing wiring diagrams from Julia code¶
Conversely, parse wiring diagrams by evaluating code in fragment of Julia language.
parsed = @parse_wiring_diagram TrigFunctions (x::R) begin
y1, y2 = sin(x), cos(x)
return y1 * y2
end
to_graphviz(parsed, orientation=LeftToRight,
node_attrs=Dict(:fontname => "Courier"))
parsed == @parse_wiring_diagram(TrigFunctions, (x::R) -> sin(x) * cos(x))
true
Application: semantics of data science code¶
Project at IBM Research AI and Stanford (Patterson, Baldini, Mojsilovic, Varshney 2018):
- Knowledge-based semantic enrichment of data science code
- Web app for Data Science Ontology + code on GitHub
analyze→
enrich→
Application: compositional assembly planning¶
Prototype project at Siemens (Master, Patterson, Yousfi, Canedo 2019):
- Planning and scheduling for automated assembly
- Toy domain: simulated LEGO assembly in Minecraft
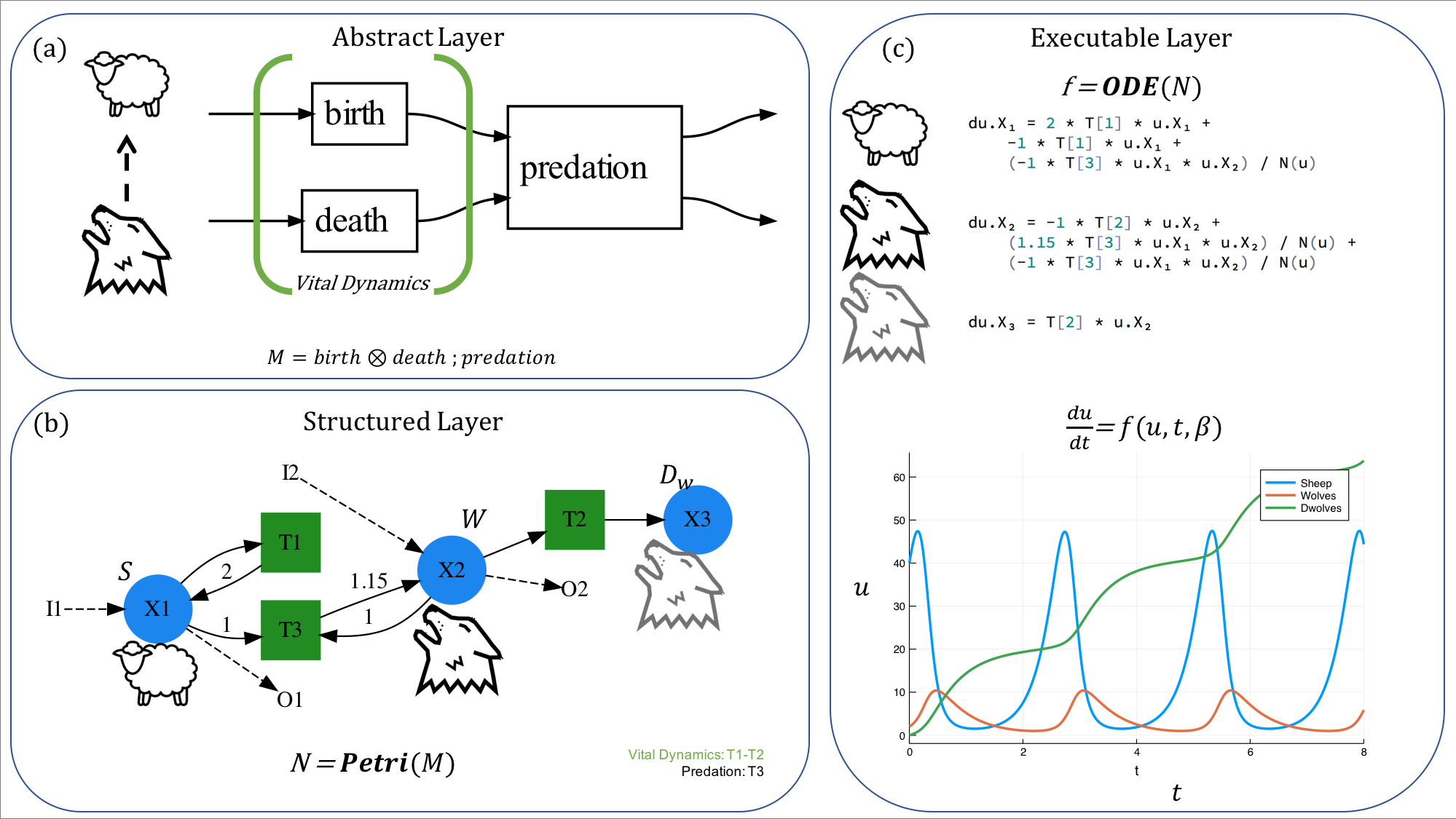
Application: scientific model augmentation¶
Ongoing project at Georgia Tech Research Institute (Halter, Herlihy, Fairbanks 2019):
- Model augmentation: transform existing scientific models to create new models
- Current focus on epidemiology (SIR, SIRS, etc): agent-based models and ODEs
- Code available as SemanticModels.jl
Future directions¶
Many! I'll just mention a few areas.
Computer algebra¶
- Declarative, rule-based rewriting for
- symbolic expressions
- wiring diagrams
- Solving word problems
- Calculating hom-sets
- GATs and beyond
- Data structures for, and operations on, GATs
- Extensions for unbiased operations, such as products and permutations
Future directions¶
"Standard library" for applied category theory¶
- Linear algebra (est. 2020!)
- Graphical linear algebra, aka linear relations
- Tensor networks and categorical quantum mechanics
- Knowledge representation
- Ologs and/or relational ologs
- Undirected wiring diagrams for relations
- Network theory: Markov processes, reaction networks, circuits, etc
- ...
Thanks!¶
Resources¶
epatters/Catlab.jl on GitHub
#catlab on the Julia Slack
Getting involved¶
I'm looking for both users and contributors. There is much to do!
Please contact me if interested.