The role of abstraction in applied math
…these are minor flaws that are easily corrected, and so the book could serve as a useful supplemental text in a graduate course using sheaf theory. It would have been better, however, if the book had never been written. (Hoobler 1977, 704)
So concludes Raymond Hoobler’s review of B. R. Tennison’s textbook on sheaves (Tennison 1975). It is a classic specimen of academic book review, taking to new heights the old joke that “really, it’s a fine book, but it’s not the one I would have written.” Book reviews in this style are only too common.1 Still, you must be wondering: what is it about this book that Hoobler finds so disagreeable? He tells us straightaway, in the opening paragraph of the review:
Perhaps the most pressing problem facing mathematics today is the increasing difficulty in communicating with nonmathematicians. The low percentage of new math Ph.D.’s with nonacademic jobs, the almost nonexistent intellectual interaction with other academic departments, and the increasingly common practise of having nonmathematicians teaching mathematics in their own disciplines illustrate this problem. In large measure it has been caused by an unhealthy overemphasis on abstraction during the past few decades. This particular book and, for that matter, all of the other books devoted solely to sheaf theory are prime examples of this overemphasis. (Hoobler 1977, 702)
While reading Hoobler’s review, I find myself agreeing with his premise but not his conclusion. Undoubtedly, there is a communication barrier between mathematicians and nonmathematicians, which is, if anything, thicker now than in the 1970s, when the review was written. Moreover, the problem of intellectual insularity is hardly confined to mathematics, but is widespread across academic disciplines. Within mathematics, Hoobler locates the problem in an “unhealthy overemphasis on abstraction” and “unnecessary generalization.” He argues that the importance of an abstract mathematical result is largely “determined by what it says about basic physical and mathematical problems.” Thus, he sees no place for a standalone exposition of sheaf theory outside the context of algebraic geometry, which was its main application at the time. I disagree. I think that the role played by abstraction in applied mathematics is considerably more nuanced than Hoobler acknowledges.
After all, why was I reading a textbook about sheaf theory? It’s certainly not because I needed sheaf theory as a technical language for algebraic geometry. Loath though I am to admit it, I couldn’t tell you the first thing about algebraic geometry.2 I’m interested in sheaf theory as a way of formalizing processes that make localized but consistent observations across space and/or time.
This idea has by now percolated into the applied fields. In pioneering work, Joseph Goguen used sheaves to model concurrency in computer systems (Goguen 1992). More recently, Michael Robinson has applied sheaf-theoretic methods to data integration and signal processing (Robinson 2017). Patrick Schultz and David Spivak use sheaves to define a logical system, called temporal type theory, in which all terms and propositions have temporal semantics, i.e., evolve over time (Schultz and Spivak 2019). These elegant applications were presumably not envisioned by the originators of sheaf theory, mainly Cartan, Serre, and Grothendieck, or by later algebraic geometers like Tennison and Hoobler.
Abstraction and concretization
The example of sheaves contains a general lesson about the nature of abstraction in applied mathematics.
Consider, in outline, the process of abstraction and concretization in mathematical research.3 In pursuit of solving some concrete mathematical problem, the mathematician develops a set of ideas and techniques. With luck, skill, and perseverance, she may solve her problem. But, in a still happier circumstance, she may realize that some of the ideas and techniques developed for her particular problem, in fact constitute a more general phenomenon. To capture the essence of this phenomenon, without the extraneous details of the original problem, she defines a new, more abstract mathematical concept. She, or possibly other researchers, develop the general theory of this new concept. The general theory is successful if it can be productively concretized in new, perhaps even unexpected, applications. All this is illustrated (in oversimplified form4) by the diagram below.
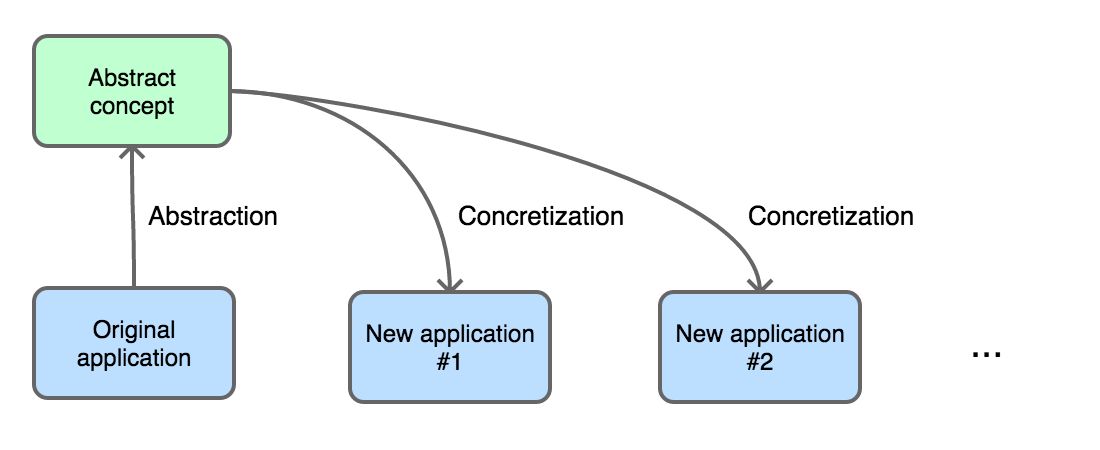
An essential aspect of this process is that new concretizations are often discovered later—sometimes much later—than the abstraction itself, by people with little or no connection to the original inventors. Sheaf theory is one example. More generally, category theory, introduced by Eilenberg and Mac Lane in the 1940s to describe constructions in algebraic topology and algebraic geometry, has developed into a general metatheory of mathematical structure. Within the burgeoning community of applied category theory, researchers model such diverse phenomena as quantum mechanics, natural language, electrical circuits, chemical reaction networks, and knowledge representation using categorical methods. I see this relatively new movement as broadening the application areas of category theory from programming languages, established in the 1980s, to many other branches of natural and computational science. As a final example, topological data analysis uses ideas from algebraic topology, particularly that of persistence, in an attempt to dissolve some classic problems in statistics, such as choosing the number of clusters in cluster analysis or choosing the smoothing parameter in density estimation.
These and other examples illustrate the remarkable reach of mathematical ideas to problems far beyond their original provenance. Granted, this optimistic view of the usefulness of mathematical abstractions probably suffers from survivorship bias: only those abstractions that are seen to be fruitful in a range of applications will survive by propagation through seminars, papers, textbooks, and informal communication. The history of mathematics is surely littered with discarded and forgotten theories. Still, I think there is something surprising about the deep interconnectedness of mathematical ideas, both within mathematics itself and within the broader STEM fields. This interconnectedness is a principal source of mathematics’ enduring beauty.
Mathematical communication
The picture of abstraction and concretization sketched above should not, I think, be too controversial, even if it is a bit oversimplified. However, judging by Hoobler’s review, its implications for mathematical communication apparently are controversial.
Because the people who discover new concretizations of a theory are often not the same people who invented the theory, it can be a valuable activity to break off conceptually independent chunks of a large theory into new, smaller theories. A non-specialist will then find it more manageable to learn the sub-theories, if they hold independent interest. Professional mathematicians have often disagreed with this assessment in particular cases. Lattice theory,5 exterior algebra,6 homological algebra,7 sheaf theory and category theory are but a few modern examples of theories that were once ridiculed for being needlessly abstract, for being “mere” languages, for failing to produce genuinely “new” results—in short, for not being real mathematics. Yet they are all now generally accepted. Many have found surprising new applications.
I have been arguing that it is valuable to abstract a sub-theory from its original context and exposit it with minimal prerequisites if it is independently interesting. Whenever there is disagreement about such matters, that last qualifier is usually the source of it. Detractors will maintain that the theory in question holds no interest outside the context where it was developed. So, for instance, Hoobler says that sheaf theory holds no interest outside algebraic topology or algebraic geometry. But it is precisely in this matter that mathematicians have been consistently refuted by history, as demonstrated by the examples above and countless others. Evidently it is no easier to predict the future in mathematics than in any other sphere of life. For this reason I take a liberal attitude towards abstraction in mathematics. Let many theories blossom. Some will develop a culture and character of their own, others will fade away. That is the natural order of things.
Even if you accept that a valid purpose of abstraction is to help diffuse important ideas throughout the mathematical and scientific disciplines, you might worry that separating abstract ideas from their original, concrete context would be a pedagogical disaster. After all, isn’t learning abstract mathematics harder than learning concrete mathematics? Counterintuitive though it may seem, I think that view is exactly backwards. Abstract math is usually easier to understand than concrete math, if it is exposited properly.
There are several reasons why this is so. First, abstract math is, almost by necessity, technically simpler than the concrete math where it originates, because the complicating details of the latter have been deliberately suppressed. You would be hard pressed to find anyone who really thinks that the proofs in algebraic geometry are simpler than in sheaf theory, or that the proofs in algebraic topology are simpler than in category theory. It is not a coincidence that number theory—which studies the lowly natural numbers, the most concrete of mathematical objects—is among the most technically formidable subjects in all of mathematics, incomprehensible even to many professional mathematicians. Algebraic structures like groups, rings, and fields, abstracted from the basic number systems, are generally easier to understand, at this level of abstraction, than are the special properties of the natural numbers, such as the distribution of the primes.
Second, abstract structures should, and usually do, have more examples than the concrete situations that inspired them. Again, this is true almost by necessity, because abstractions loosen constraints previously taken to be binding. So one would think that expositions of abstract math ought to contain more examples, not fewer, than those of concrete math. Students of mathematics know that this happy thought does not often survive contact with reality. In mathematical writing, abstract theory often goes along with a severe austerity of style, where examples and informal explanations are scorned. However, this is a failing of mathematical culture, not of mathematics itself. The best expositors of mathematics (and of every other subject) have always understood that a healthy supply of examples is crucial for understanding.
Conclusion
I agree with Hoobler that mathematicians are struggling to communicate effectively with nonmathematicians. This state of affairs harms mathematics, by depriving it of prestige and thus, ultimately, of funding and resources. It harms other STEM fields, by depriving them of conceptual tools for systematically organizing knowledge and rigorously formulating problems. But Hoobler’s diagnosis, that mathematics overemphasizes abstraction, misses the mark. Abstraction is an essential element of the mathematical process, that both simplifies mathematical concepts and extends their reach. Instead of eschewing abstraction, expositors of math should embrace it, but they should also try to minimize prerequisites, provide informal explanations as well as proofs, use pictures and graphics liberally, and illustrate abstract concepts with examples as diverse and numerous as possible. Only in this way will beautiful mathematics escape the math department.
I am encouraged that the last few years have witnessed an uptick in “applied” expositions of traditionally “pure” subjects. For example, in topology, see Robert Ghrist’s Elementary Applied Topology (Ghrist 2014) and in category theory, see David Spivak’s Category Theory for the Sciences (Spivak 2014) and Fong and Spivak’s textbook Seven Sketches in Compositionality (Fong and Spivak 2019). John Baez is currently guiding an informal online course based on the last book. It would be going too far to say that all mathematical exposition should be in this style, but given the current severe imbalance, these contributions are warmly welcomed.
References
Footnotes
Academics are notorious for coopting book reviews to promote their personal ideologies. Although sometimes entertaining, this tendency is a form of professional narcissim. People read book reviews to learn about the book under review, not the reviewer’s assorted beliefs and prejudices.↩︎
A nonmathematician might be surprised to learn that algebraic geometry is the “concrete” application justifying the existence of the “abstract” theory of sheaves. For most of us, applications happen in subjects like physics, chemistry, computer science, and electrical engineering. For Hoobler, sheaf theory is abstract, while algebraic geometry is concrete—or at least concrete enough to be “real mathematics.” All this goes to show that abstractness is not an absolute or universal notion. What is considered abstract depends on contingent historical, social, and personal factors.↩︎
Intriguingly, an analogous process of generalization and specialization seems to be essential to the empirical sciences, on which more in a later essay.↩︎
This picture of abstraction and concretization is oversimplified in many ways. We have already seen that abstractness is a relative notion. Mathematical abstractions also exist at many different levels, in an endlessly rich web of concepts, subconcepts, embeddings, and deformations. A better picture would somehow illustrate these structures of hierarchy and meronomy.↩︎
See (Rota 1997b) and for more anecdotes about lattice theory also (Rota 1997a, 51–54).↩︎
See Rota’s essay on “Hermann Grassmann and Exterior Algebra” (Rota 1997a, 46–48).↩︎
In lieu of giving any exercises in Ch. IV of his Algebra, 2nd ed., Serge Lang writes: “Take any book on homological algebra, and prove all the theorems without looking at the proofs given in that book. Homological algebra was invented by Eilenberg-MacLane. General category theory (i.e. the theory of arrow-theoretic results) is generally known as abstract nonsense (the terminology is due to Steenrod)” (p. 175). Lang’s Algebra is the standard graduate-level textbook on abstract algebra.↩︎